Here are three lines intersecting at a point:

Well, actually, it’s not.

As any engineer will tell you, it isn’t quite like that, it looks like this:

There is always a slight error.

In fact, when you get closer, it looks like this:

Actually, nobody ever drew a straight line anyway, they all look like this, if you get close enough:

But, then again, a line is mathematical and has only one dimension, length. No thickness, so a line actually looks like this:

Useful, innit?

Alright, stop messing about.

Lines and curves are mathematical concepts that only exist in Mathspace.

In order to help us understand and make sense of the universe we see, we trace out lines on paper, etc. using a straight edge. The tip of the pencil follows a line as closely  as the straight edge will allow and leaves a trace on the paper which we use as a picture of the line we were thinking about in Mathspace. OK, use a laser, whatever, the principle is the same.

In order to take this further, we have to accept that the illustrations do show lines, pictures of them, and that we have added thickness to make the traces visible.

Now, what we are talking about is “pictures” of curves and lines. The actual things themselves are the loci of points following a mathematical curve or interpreting and equation.

Now we have another  problem.

Nobody has ever drawn a circle.

It looks like this:

And of course it gets worse.

Nobody has ever drawn a closed curve.

The surface they are tracing a locus on is moving, spinning around the Earth, trundling round the Sun and wobbling through the galaxy.

It might look more like this:

It should look a bit like a helical spring, or a slinky. Remember, what we are looking at are pictures of curves and lines. Also, this is an analogy, it helps to make a point by stripping out a lot of stuff. It may  not be accurate, but if you’ll forgive me, you get my drift.

This does not need to worry us. We do not live in Mathspace. We live in Realspace and we only need to dip into Mathspace to help us understand, interpret and, with luck, predict things in Realspace.

Now, just in case you haven’t fallen asleep yet.

This is a Timeline:

An Event has happened at a time on our timeline. But where, or when?

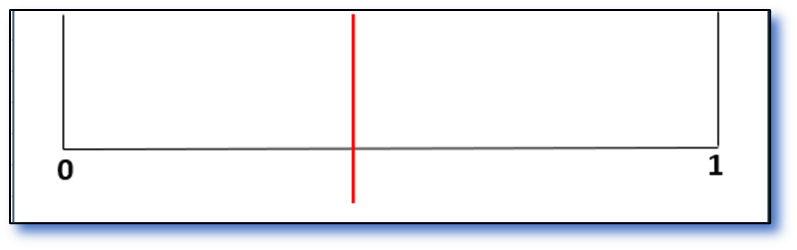
This is the same event, but labelled with two times, 0 and 1. But the event is somewhere in between.

Easy , put in more divisions:

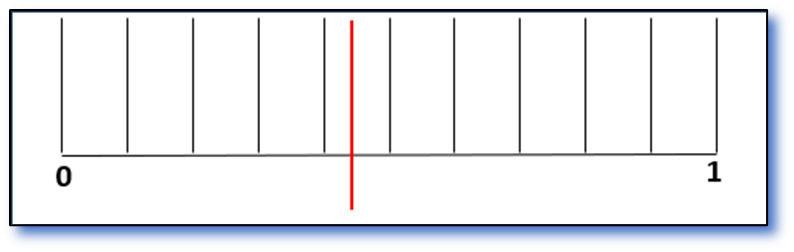
Damn, missed ‘em all. Somewhere between 0.4 and 0.5. Easy, do it again:

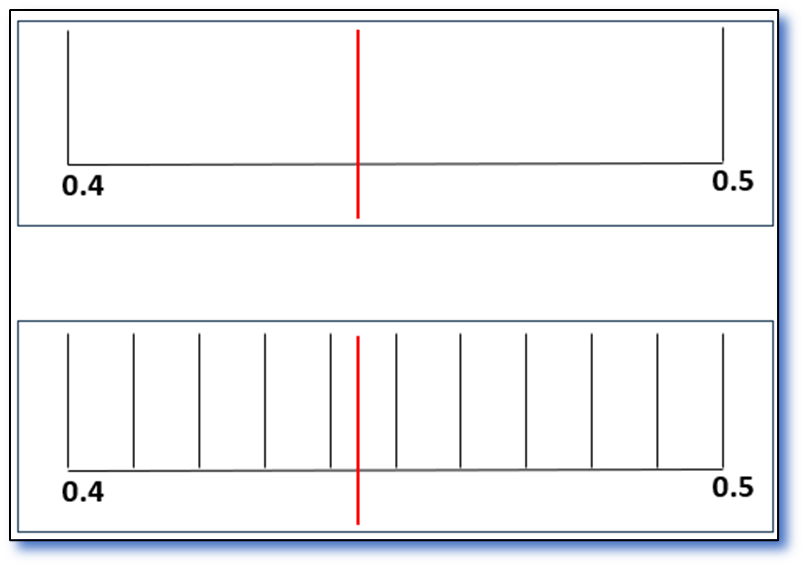
Dammit, try again:

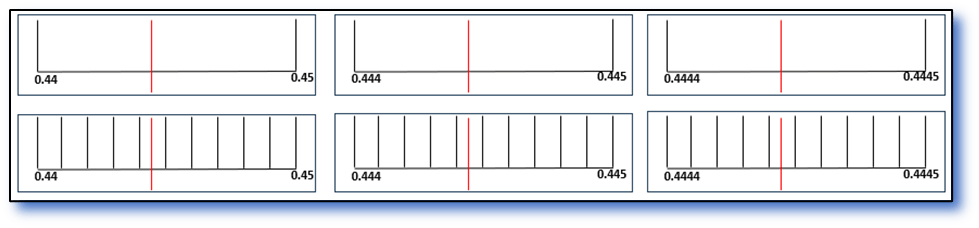
Still no luck.

If we do it an infinite (oh not him again) number of times, it’s going to look like this.

Nailed it!

Not really.

Take all those grid lines and sweep them up to the left.

Can’t really show it. These are Mathematical lines. They have no thickness. That means even when there is an infinite number of them, there will be as much empty space on the timeline as before.

That chance of an event crossing the Timeline on one of an infinite number of subdivisions, is NIL.

But it gets worse. Or better depending on how you look at it.

It follows that the chance of two events crossing the timeline at the same point is also nil.

And that means the chance of any two events happening at the same time, anywhere, any time is nil. Throughout the Universe.

This means it is possible that there is a single sequence of events happening throughout the Universe. That consecutive events happen at the opposite ends of the Universe doesn’t matter.

I think I need to stop here.

This bit was easy. The next bit requires a little thought, a lot of coffee and some smokes.

OK, a glass of red clinched the deal.

The next steps are too far to be tagged on here. They need to be dealt with separately.